- Original Article
- Open access
- Published:
Geometric analysis of concept vectors based on similarity values
Lingua Sinica volume 3, Article number: 12 (2017)
Abstract
In this paper, we offer a geometric framework for the computing of a concept’s conceptual vector based on its similarity position with other concepts in a vector space called concept space, which is a set of concept vectors together with a distance function derived from a similarity model. We show that there exists an isometry to map a concept space to a Euclidean space. So, the concept vector can be mapped to a coordinate in a Euclidean space and vice versa. Therefore, given only the similarity position of a concept, we can locate its coordinate and its concept vector subsequently, using distance geometry methods. We prove that such mapping functions do exist under some conditions. We also discuss how to map non-numerical attributes. At last, we show some preliminary experimental results and thoughts in the implementation of an attribute mining task. This work will benefit attribute retrieval tasks.
1 Introduction
For semantic computing tasks, the fundamental step is to represent and acquire the meaning of individual words. The representation of the meaning can either be a lexical ontology such as WordNet (Fellbaum 1998), an attribute-based structure (Blackburn 1993), or a distributional semantic model such as word vector model (Erk 2012; Turney and Pantel 2010). All the representations have their own advantages. Ontologies and attribute-based models encode explicit human-readable knowledge, while word vector models offer a good computation framework based on vector spaces. Therefore, it may be desirable to combine the attribute-based structure with vector space models.
In this paper, we offer a framework to compute concept vectors, which is an attribute-based semantic representation, in a vector space whose distance metric is defined by the similarity values of words. Usually, in natural language processing (NLP), similarity measurement is an outcome of algorithms based on semantic representation like a lexical ontology or a word vector (Finkelstein et al. 2001). However, it is also interesting to see if we can turn our head to the other direction, i.e., using similarity values as input to construct semantic representation. As mentioned by Turney (2006), the amount of attributional similarity (i.e., semantic relatedness) between two words, A and B, depends on the degree of correspondence between the properties of A and B. Consequently, there will be some identical parts in the conceptual vectors of A and B. The questions are the following: which parts are the same in the two vectors? Is there a way to compute it? If these two questions could be addressed, we can calculate a word’s unknown concept vector by the concept vectors of its similar words.
The contribution of this paper resides in several aspects. First, we use similarity values to induce semantic structures for words, not vice versa as most previous works. Second, unlike previous studies in attribute retrieval, we provide a mathematical framework to compute an unknown concept vector based on its distances with other instances in a vector space. Third, we prove that the framework is viable and show that the constraints could be met in real applications.
The paper is structured as the following. The next section is concerned mainly about related works. Then, we introduce the basic concepts of concept space and similarity position as well as a walk-through example in Section 3. After that, we discuss the relation between similarity and distance. In Sections 5 and 6, we shall prove that there is an isometry from a concept space to a Euclidean space under given conditions, which could be met in real applications. Based on the isometry, we show a method to find the attributes of a concept given its similarity position with other concepts. Section 7 shall be devoted to some discussions about non-numerical attributes, while in Section 8, we may show a mini example and some preliminary experimental results. The last section is the conclusion.
2 Related works
2.1 Vector representation of lexical semantics
A lot of researchers represent word meaning by vectors. A category of prevalent models is the distributional semantics models (DSMs), which are also known as word space models (WSMs) (Baroni and Lenci 2010, 2011). These models are motivated by the distributional hypothesis (Harris 1954), which states that words occurring in similar contexts are semantically similar. Therefore, a word’s meaning is presented by a context vector in which each dimension encodes co-occurrence information of the word in a corpus. The context vectors need to be adjusted to counter the problems of high dimensionality and data sparseness (Sahlgren 2005) or to be trained from a corpus (Baroni et al. 2014). A number of NLP tasks could be handled as the computing of vectors in a vector space, such as similarity measurement for short texts (Mihalcea et al. 2006), antonym-synonym discrimination (Santus et al. 2014), semantic composition (Mitchell and Lapata 2008), etc. (Turney and Pantel 2010) and Erk (2012), have given two detailed surveys on these models.
Though DSM is nearly the synonym for vector space models, there are other kinds of vector representation. Some researchers believe that human subjects can generate lists of defining features (McRae et al. 2005; Vigliocco et al. 2004). Baroni et al. (2010) suggests extracting a property list from a corpus which can be used as a vector space representation. A model related to our paper to more extent is the conceptual space model suggested by (Gärdenfors 2004, 2014). In a conceptual space, each dimension stands for a quality, such as the hue, saturation, and brightness of a color. So, each point is an entity or property. The similarity of two entities is defined as a function of the distance between two points in the space. There are some implementations of conceptual spaces, while some in knowledge representation and reasoning (Frixione and Lieto 2013; Gärdenfors and Williams 2001; Lieto et al. 2015), others in spatial information systems (Adams and Raubal 2009; Janowicz et al. 2012; Raubal 2004).
There are some main differences between our work and previous vector representations. Firstly, our representation of word meaning actually has two levels: the explicit level of concept vector which is similar to a property (attribute) list and an implicit level of similarity position, which could be viewed as an “untraditional” distributional vector in which each dimension is the similarity with other words. Secondly, compared with Gärdenfors’ work, this paper focuses on the computation of concept vectors, while Gärdenfors’ work is in the cognitive science domain and “not developing algorithms” as noted in the preface of Gärdenfors (2004).
2.2 Semantic similarity and its calculation
Similarity is a widely used notion in different subjects. Previous reserachers (Gentner 1983; Medin et al. 1990; Turney 2006) state that there are two types of similarity: attributional similarity, which is the correspondence between attributes, and relational similarity, which is the correspondence between relations. Turney and Pantel (2010) mention that attributional similarity is equivalent to semantic relatedness (Budanitsky and Hirst 2001) in computational linguistics, and semantic similarity should involve in both attributional and relational similarity.
The majority of researchers have put emphasis on the similarity of words. In psychological experiments, the semantic similarity between two words is a fixed value computed from the average of the annotated values given by a group of subjects (Miller and Charles 1991), while in NLP applications, the similarity is calculated by various algorithms. A popular category of models uses a lexical ontology as the resource, such as WordNet. These methods usually depend on the distance between two concepts in the ontology (Li et al. 2003; Resnik 1995; Wu and Palmer 1994), ontological features (Petrakis et al. 2006; Rodríguez and Egenhofer 2003; Sánchez et al. 2012), or information content (Jiang and Conrath 1997; Liu et al. 2012). Varelas et al. (2005) have provided an evaluation of such methods.
Some researchers utilized contextual information in similarity computing. Such information is usually extracted from a corpus. Jiang and Conrath (1997) used corpus statistics as a correction for edge-counting methods. Li et al. (2003) combined the information from WordNet and corpus. Gao et al. (2015) introduced another model combining edge-counting and information content. Researchers in DSM used word similarity measurement as an benchmark task, in which the similarity of words were measured as the similarity of the correspondent word vectors (Agirre et al. 2009; Baroni et al. 2014; Erk 2012; Mihalcea et al. 2006; Turney and Pantel 2010). For vector-based methods, the most popular way to compare vectors is vector cosine (Turney and Pantel 2010). Other widely used methods include geometric measures like Euclidean distance, Manhattan distance, measures from information theory (Bullinaria and Levy 2007), and more recent methods like APSyn (Santus et al. 2016). Besides corpus, other contextual information like Web information are used as well. Researchers based their calculation on variations of Web co-occurrence (Chen et al. 2006; Han et al. 2013a) or snippets from search engines (Bollegala et al. 2007).
For cognitive scientists, similarity between concepts is also a main topic. Many researchers suggest that similarity be viewed as a function of distance (Gärdenfors 2004; Hahn and Chater 1997; Nosofsky 1992; Reisberg 2013; Shepard 1987). Models derived from such an assumption is called a geometric model of similarity. If we apply the geometric model to words, the similarity between two words could be calculated from the distance of two attribute vectors in a conceptual space (Gärdenfors 2004). It has to be noted that the geometric model has been criticized by some researchers, most famously by Tversky (1977), who has suggested feature model instead, in which similarity is not measured by distance, but by two concepts’ common and distinct features. One of Tversky’s criticism is on the symmetry axiom (Hahn and Chater 1997) of the geometric model. Tversky showed that Tel Aviv is more similar to New York than New York is similar to Tel Aviv. Gärdenfors (2004) has responded to this criticism, stating that the weight of dimensions in the attribute vector is different between when comparing Tel Aviv with New York and when comparing New York with Tel Aviv.
2.3 Attribute mining approaches
The framework of this paper could be applied to attribute mining tasks directly. The majority of works in attribute mining focus on extracting values for pre-specified attributes, such as person names. There is a sub-task of WePS (Web People Search Workshop) (Artiles et al. 2010; Artiles et al. 2009) concerning the extraction of affiliation (Nagy et al. 2009), gender, and profession (Tokunaga et al. 2005) of people. Besides the extraction of person attributes, there are also some works on product property extraction, such as Ghani et al. (2006) and Probst et al. (2007), in which the researchers extracted “attribute-value” pairs from product descriptions. Such methods have been widely used in opinion mining tasks for products, such as Pang and Lee (2008) and Liu (2011).
The resources from which the researchers extracted attributes also differ. Some researchers (Brin 1999; Kopliku et al. 2011; Sekine 2008; Suchanek et al. 2008) analyzed structured or semi-structured text, such as HTML tables and encyclopedias. Others (Bellare et al. 2007; Pasca and Benjamin V. Durme 2007; Tokunaga et al. 2005) used a corpus or Web text. They usually used lexico-syntactic templates for the extraction. Only a few researchers started to use similarity as a tool for attribute retrieval, such as Alfonseca et al. (2010) and Liu and Duan (2015).
3 Basic notions and a walk-through example
3.1 The scope of our task
In this paper, we will compute word meaning by similarity. Before entering into details, we would like to define the scope of our task.
Firstly, we take the cognitive view of meaning, which states that the meaning of a word is a mental entity (Gärdenfors 2004): a concept. Hereafter in this paper, we use the term “concept” to denote word meaning. To save our framework from the details of a language, we are computing concepts, not words. Moreover, we use a concept vector to represent each concept. Dimensions of the vector represent attributes, which are mathematical specifications of the concept’s properties.
Secondly, we view (semantic) similarity as the synonym of attributional similarity since we do not include the relation of word pairs in our framework. Consequently, the “gold” similarity of two concepts ought to be decided by their attributes, i.e., concept vectors. Since the target concept vector is unknown to our task, we approximate the gold similarity by selected similarity computing algorithms.
Finally, we take the geometric view of similarity despite the previous critics. The reason is that we are not seeking a perfect representation of similarity, as our work is more focused on the implementation/computing level. We believe the geometric model is a good enough approximation of similarity at this time. Moreover, since the similarity values are generated by algorithms in our framework, we can also pick similarity algorithms which conform to conditions in Section 4, which guarantees the algorithm is close to a geometric model.
3.2 Basic definitions
While we are taking into discussion of an attribute in a concept vector, we are referring to the attribute name and value together. The name is a natural number which is an index in the vector, and the value is a real number. At this step, we shall also assume that the values are all real number values. We will discuss the case of non-numerical values, such as string values in Section 7. We also assume that all attributes have only one value, not multiple values.
Formally, let C be a set of all concepts within a domain. If we have an order on the set of all the possible attributes in C, we can construct the representation of the concept c as a vector of values while the subscripts of the vector components correspond to attribute names.
Definition 1
The concept vector of a concept c is a vector v=(v 1,v 2,…,v N ), in which N is the number of attributes in C and v i is the value of the ith attribute.
Definition 2
A concept space is a pair \((\mathfrak {C},\mathrm {t}\circ \mathrm {s})\), in which \(\mathfrak {C}\) is a set of concept vectors and d=t∘s is a distance function derived from the similarity model s and the transformation function t.
In Definition 2, a similarity model outputs a similarity value for two concepts. We will discuss it in detail later. The concept space can also be viewed as a set of “known” concept vectors and their distances. When there is no ambiguity, we will use \(\mathfrak {C}\) to denote the whole concept space.
We will also introduce the zero vector 0 whose components are all 0s for the sake of further calculations.
Sometimes, a concept can be represented by an “attribute-value structure” (AVS), which contains attributes and their values can also be an AVS. For recursive values, we “flatten” the AVS to be a vector of attribute-value pairs, {〈a 1,v 1〉,〈a 2,v 2〉,…,〈a N ,v N 〉}. A possible method for flattening is to join the attribute names from the root of the AVS to the deepest value. For example, in a LAPTOP concept, we can have an attribute cpu, while the value of cpu is another concept INTEL CORE, which has an attribute speed with the value of 2.4 G. Then, the speed attribute denoted as LAPTOP.cpu.speed in a recursive AVS could be rewritten as LAPTOP.cpu_speed which is a direct attribute under the concept LAPTOP.
A word similarity computing method can be taken as a function. Consequently, we have the following definition of a similarity model for our paper, which inputs could be concept vectors or concepts (without their vectors). A similarity model could be annotation-based or algorithm-based.
Definition 3
A similarity model is a function \(\mathrm {s_{i}} \colon \mathbf {C}\cup \mathfrak {C}\times \mathbf {C}\cup \mathfrak {C} \to [0,1]\). S is the set of all similarity models.
In fact, a similarity model in Definition 3 is a similarity computing algorithm. Though the input is a concept by definition, in practice, it will be a correspondent word in a specified language.
Given a concept space and a similarity model, we have the following definition of the similarity position of a concept c u .
Definition 4
The similarity position sp of c u in concept space \((\mathfrak {C},\mathrm {t}\circ \mathrm {s_{i}})\) is defined as:
In the above definition, \(\boldsymbol {v_{i}}\in \mathfrak {C}\) for i∈[1,M]. The set of all similarity positions is denoted as \(\mathfrak {P}\).
3.3 An outline of our framework by a walk-through example
In order to illustrate our work better, we would like to give a sketch of our framework taking a very simple example which will also be used over the next two sections. The main target of this paper is to solve the following problem:
Problem 1
Given:
-
1.
A concept space \((\mathfrak {C},\mathrm {t\circ s})\) whose size is M.
-
2.
A similarity position sp whose correspondent concept vector is vp.
We want to find a function g s.t. \(\mathrm {g}(\mathfrak {C}, \mathrm {t\circ s}, \boldsymbol {sp})=\boldsymbol {vp}\).
Just let us try to suppose all concepts in one domain have only two attributes: “can_fly” and “can_swim”. We have three known concepts which are swan, butterfly, and fish. So, the correspondent concept space \(\mathfrak {C'}\) is consisted of three concept vectors v 1 , v 2 , and v 3 respectively:
Suppose there exists a similarity function s which will produce similarity values for each concept pair. Please be noted that we may not know the mechanism of the similarity function but only the values, which is shown in a similarity matrix S below in which S ij =s(v i ,v j ).
Now, we have an unknown concept x. We do not know its concept vector v 0 . In other words, we do not know its attributes. However, we know its similarity values with other concepts according to observation, and the values are generated by the same similarity function aforementioned. The similarity position of x is (0,0.1056,0.5528). We want to solve v 0 in the steps below:
-
1.
Transform the similarity values to distance values in \(\mathfrak {C'}\).
-
2.
It is obvious to see that \(\mathfrak {C'}\) is not a Euclidean space. Since it is easier to do algebra in Euclidean spaces, we will first try to transform \(\mathfrak {C'}\) to a Euclidean space \(\mathfrak {D'}\).
-
3.
In \(\mathfrak {D'}\), we will locate the coordinate of x by its distance with other points using distance geometry methods. Then, we will convert the coordinate in \(\mathfrak {D'}\) to that in \(\mathfrak {C'}\), which is our target v x .
In the following three sections, we will illustrate and prove the viability of the above three steps.
4 Similarity as a function of distance
As mentioned in Section 3, we adopt a geometric view of similarity. So, similarity is taken as a function of distance. Previous researchers in psychology suggest that similarity be viewed as an exponentially decaying function of distance (Gärdenfors 2004; Hahn and Chater 1997; Nosofsky 1992; Reisberg 2013; Shepard 1987).
In Eq. 2, c is the decay factor.
Nosofsky (1986) argues that the above function should be a Gaussian function.
In the area of computational linguistics, Jin et al. (2014) showed that a function of word similarity meets the properties for a distance metric. The relation between similarity function and distance function is as follows:
We model the transformation between a similarity model and a distance function using a transformation function.
Definition 5
A function t:[0,1]→[0,1] is a transformation function, if there is a pair of similarity model s and distance function d s.t. d=t∘s and s=t −1∘d.
However, for a similarity model in NLP, it is not necessarily a function of distance unless it satisfies some basic properties. It is well-known that there are three defining properties for a distance function:
-
(Reflexive) d(x,x)=0
-
(Symmetric) d(x,y)=d(y,x)
-
(Triangle inequality) d(x,y)+d(y,z)≥d(x,z)
We will show two examples that satisfy the above properties first.
Example 1
The similarity function for the walk-through example is a function of distance.
Just set the transformation function as t(x)=1−x. It is easy to see that the resulting distances in the walk-through example are symmetric and reflexive. Furthermore, we can see that the distances (0.4472, 0.8944, 1) conform to the triangle inequality property. So, t∘s is a distance function.
Example 2
Any similarity model based on edge counting is a function of distance.
The “edge counting” methods, which calculate similarity based on the distance of two concepts on the hierarchy, are a common family of similarity models. Let e(c 1,c 2) be the number of edges of c 1 and c 2 on the hierarchy; it is obvious that e is a distance function. So, any similarity function s e =t e ∘e is by definition a function of distance. If t e also has an inverse function, it is a transformation function.
Theorem 1
If t(x)=1−x, d=t∘s i is a distance function ⇔
-
1.
s i (x,x)=0
-
2.
s i (x,y)=s i (y,x)
-
3.
s i (x,y)+s i (y,z)≤s i (x,z)+1
Proof
1 The proof of properties 1 and 2 is obvious.
If properties 1 and 2 hold, then from the defining properties of a distance function, we know d is a distance function ⇔ d(x,y)+d(y,z)≥d(x,z).
Theorem 2
If \(\mathrm {t}(x)=-\frac {1}{c}\ln {x}\), d=t∘s i is a distance metric ⇔
-
s i (x,x)=0
-
s i (x,y)=s i (y,x)
-
s i (x,y)·s i (y,z)≤s i (x,z)
Proof
Omitted. □
5 Mapping from concept spaces to Euclidean spaces
5.1 The general case
To compute within concept spaces, we would like to map them to some spaces we are familiar with: Euclidean spaces. We will first show the general constraints for a concept space to be isometric to a Euclidean space. In other words, we will show that the mapping is possible by proofs.
Theorem 3
Let \((\mathfrak {C},\mathrm {d})\) be a concept space. There exists an isometry  , if the following constraints are met:
, if the following constraints are met:
-
1.
(Finite dimension)
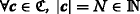
-
2.
(Translation invariance) \(\forall \boldsymbol {x}, \boldsymbol {y}, \boldsymbol {u} \in \mathfrak {C},\ \mathrm {d}(\boldsymbol {x},\boldsymbol {y})=\mathrm {d}(\boldsymbol {x}+\boldsymbol {u},\boldsymbol {y}+\boldsymbol {u})\)
-
3.
(Scaling invariance)
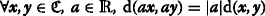
Proof
We will first prove \(\mathfrak {C}\) is a normed space. By the definition of a concept space, d is a distance function. Therefore, \((\mathfrak {C},\mathrm {d})\) is a metric space. Since we have constraints 2 and 3, we can induce a norm function p(x)=d(x−0) which satisfies the norm definition. Consequently, \((\mathfrak {C},\mathrm {p})\) is a normed space.
Because \((\mathfrak {C},\mathrm {d})\) is a N-dimensional normed space, it is isometric to all N-dimensional normed spaces as long as  . Since
. Since  is also an N-dimensional normed space, \(\mathfrak {C}\) is isometric to
is also an N-dimensional normed space, \(\mathfrak {C}\) is isometric to  . □
. □
In the following subsections, we will show that the constraints of translation and scaling invariance can be met for concept spaces with some simple conditions.
Since f is an isometry, it has two useful properties.
Corollary 1
d(c 1 ,c 2 )=∥f(c 1 ),f(c 2 )∥2, in which ∥·∥2 is the Euclidean distance.
Corollary 2
f has an inverse function.
5.2 The scaling and translation invariance conditions
Following the definition of subsumption of metric spaces, we say that a concept space \((\mathfrak {C'},\mathrm {d'})\) is a hyperset of \((\mathfrak {C},\mathrm {d})\) if and only if \(\mathfrak {C}\subseteq \mathfrak {C'}\) and d⊆d. Obviously, if we can find a hyperset of \(\mathfrak {C}\) that is isometric to  , Corollary 1 is true for all concept vectors in \(\mathfrak {C}\). Therefore, our target now is to find a hyperset of \(\mathfrak {C}\) that is scaling and translation invariant.
, Corollary 1 is true for all concept vectors in \(\mathfrak {C}\). Therefore, our target now is to find a hyperset of \(\mathfrak {C}\) that is scaling and translation invariant.
Theorem 4
Let \((\mathfrak {C},\mathrm {d})\) be a concept space. There exists a hyperset \((\mathfrak {C'},\mathrm {d'})\) of \((\mathfrak {C},\mathrm {d})\) which is scaling invariant if \(\mathfrak {C}\) is finite and there is a boolean attribute.
Proof
We want to prove  . Let us construct the \((\mathfrak {C'},\mathrm {d'})=(\mathfrak {C},\mathrm {d})\) initially.
. Let us construct the \((\mathfrak {C'},\mathrm {d'})=(\mathfrak {C},\mathrm {d})\) initially.
If a=0, d(a x,a y)=d(0,0)=0=0·d(x,y).
If a=1, obviously, it is true.
If a≠0 or a≠1, since there is a boolean attribute, \(a\boldsymbol {x}\not \in \mathfrak {C}\) and \(a\boldsymbol {y} \not \in \mathfrak {C}\). Therefore, let \(\mathfrak {C'}=\mathfrak {C}\cup {a\boldsymbol {x}, a\boldsymbol {y}}\) and d ′(a x,a y)=|a|d ′(x,y). Since \(\mathfrak {C}\) is finite, by this manner, we can construct a scaling invariant \((\mathfrak {C'},\mathrm {d'})\). □
In practice, any concept space is within a domain and is finite; otherwise, it is not computable. Moreover, it is reasonable to assume that at least one, if not the majority, of the attributes is boolean.
Different from scaling invariance, the constraint for translation invariance seems to be stricter. To begin with, we will first introduce a property on distance functions. A distance function d on the concept space \(\mathfrak {C}\) is decomposable if the value of d(x) is decided by the attributes of x independently. In other words, \(\mathrm {d}(\boldsymbol {v_{1}},\boldsymbol {v_{2}})=\tilde {\mathrm {d}}(\boldsymbol {k})\), in which k i =τ i (v 1i ,v 2i ). It is reasonable to imagine that τ i is a kind of distance function on the values of an attribute.
Theorem 5
Let \((\mathfrak {C},\mathrm {d})\) be a finite concept space. There exists a hyperset \((\mathfrak {C'},\mathrm {d'})\) of \((\mathfrak {C},\mathrm {d})\) which is translation invariant if:
-
1.
d is decomposable, i.e. \(\forall \boldsymbol {v_{1}},\boldsymbol {v_{2}}\in \mathfrak {C}, \mathrm {d}(\boldsymbol {v_{1}},\boldsymbol {v_{2}})=\tilde {\mathrm {d}}(\boldsymbol {k})\), in which k i =τ i (v 1i ,v 2i ).
-
2.
Each function τ i is translational invariant, i.e.
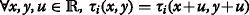 .
.
Proof
Let us construct \((\mathfrak {C'},\mathrm {d'})=(\mathfrak {C},\mathrm {d})\) initially.
If v 1 +u and \(\boldsymbol {v_{2}}+\boldsymbol {u}\in \mathfrak {C}\), \(\mathrm {d}(\boldsymbol {v_{1}}+\boldsymbol {u},\boldsymbol {v_{2}}+\boldsymbol {u})=\tilde {\mathrm {d}}(\tau _{1}(v_{11}+u_{1},v_{21}+u_{1}), \ldots, \tau _{N}(v_{1N}+u_{N},v_{2N}+u_{N}))\). Because τ i is translation invariant, the above equation equals to \(\tilde {\mathrm {d}}(\tau _{1}(v_{11},v_{21}), \ldots, \tau _{N}(v_{1N},v_{2N}))=\mathrm {d}(\boldsymbol {v_{1}},\boldsymbol {v_{2}})\).
If v 1 +u or v 2 +u does not belong to \(\mathfrak {C}\), let us first assume \(\boldsymbol {v_{1}}+\boldsymbol {u}\not \in \mathfrak {C}\). We just let \(\mathfrak {C'}=\mathfrak {C}\cup {\boldsymbol {v_{1}}+\boldsymbol {u}}\) and set d ′(v 1 +u,v 2 +u)=d(v 1 ,v 2 ). If \(\boldsymbol {v_{2}}+\boldsymbol {u}\not \in \mathfrak {C}\), add v 2 +u to \(\mathfrak {C'}\) and set the value of d ′ accordingly. □
The intuitive for the above theorem is straightforward. If the distance function is the combination of distance functions of each attribute, the translation invariance condition is now imposed on these distance functions on attribute values, which is much easier to verify. It is reasonable to assume that there exist some attribute-level distance functions derived from the Euclidean distance on  . So, we have the following corollary.
. So, we have the following corollary.
Corollary 3
A finite concept space \((\mathfrak {C},\mathrm {d})\) in which d is decomposable has a translation invariant hyperset if \(\forall i\ \tau _{i}(a,b)=\tilde {\tau _{i}}(|a-b|)\), in which \(\tilde {\tau _{i}}\) is a function on  .
.
Proof
For any  , \(\tau _{i}(x+u,y+u)=\tilde {\tau _{i}}(|x+u-y-u|)=\tilde {\tau _{i}}(|x-y|)=\tau _{i}(x,y)\). □
, \(\tau _{i}(x+u,y+u)=\tilde {\tau _{i}}(|x+u-y-u|)=\tilde {\tau _{i}}(|x-y|)=\tau _{i}(x,y)\). □
As we have discussed before, boolean attributes are common in concepts. For these attributes, there is a more direct necessary constraint for translation invariance.
Corollary 4
If the finite concept space \((\mathfrak {C},\mathrm {d})\) has boolean attributes, e.g., the ith component of the concept vector, \(\mathfrak {C}\) is translation invariant only if τ i (0,0)=τ i (1,1).
Proof
Omitted. □
5.3 The linear approximation of isometry
On the implementation level, an easy guess of the isometry function f is that it may be (or be approximated by) a linear weighting function since different attributes contribute differently to similarity. Researchers in cognitive science have such assumptions (Gärdenfors 2004).
Let us return to the walk-through example. Suppose the weight vector is (w 1,w 2). So, the isometric function is f(v)=(w 1 v 1,w 2 v 2). We can have the following equations:
Substitute d(v 1 ,v 2 ), d(v 2 ,v 3 ), v 1 , and v 2 with their values, we will have a system of linear equations.
Since w 1 and w 2 are positive, we get w 1=0.4472 and w 2=0.8944.
In order to give a general solution, we will first introduce the following definition.
Definition 6
A weight matrix W i =(w ij ) N×N is a diagonal matrix depending on the similarity model s i , where
Please be noted that weight matrix is equivalent to a weight vector. We use matrix because it is easier to represent in terms of matrix calculation.
For an isometry f, we just assume that we can find a weight matrix W i such that for any \(\boldsymbol {v}\in \mathfrak {C}\), f(v)=W i ·v T.
Let v 1 =(v 11,…,v 1N ) and v 2 =(v 21,…,v 2N ). Since f is an isometry, from Corollary 1, we have the following:
Suppose we have M concepts and N attributes in the concept space. Let us introduce the following definitions.
Definition 7
The subscript vector r=((1,1),(1,2),…,(1,M),(2,3),…,(2,M),…, (M−1,M)).
r is a vector of all possible combination of two subscripts in a concept space \(\mathfrak {C}\).
Definition 8
The coefficient matrix A=(a ij ) M(M−1)/2×N , where \(\phantom {\dot {i}\!}a_{ij}=(v_{r_{i1}j}-v_{r_{i2}j})^{2}\).
Here, r i1 means the first number of the ith component of r. v xy means the yth component of v x . Similarly, the support vector b is a M(M−1)/2×1 matrix. Let denote d(v i ,v j ) as d i,j .
The augmented matrix B=[A,b ] is a row block matrix consisting of A and b.
Theorem 6
Given a concept space \(\mathfrak {C}\), there exists a weight matrix W i satisfying
if rank(A)=rank(B)=N.
Proof
Let w be a matrix of N×1. A·w=b is a linear equation system.
Since rank(A)=rank(B)=N, there exists the only solution w 0 ={w 1,w 2,…, w k ,…,w N }. So, for any two concept vectors v u and v v , there is one correspondent linear equation:
Let us construct W i from w s.t. w kk =w k . Rewriting the left-hand side of the equation, we will have
Since d(v u ,v v ) is positive, we reach our target. □
There are two notes related to the above theorem. First, as our condition in Theorem 6 is quite strong, we may get the slack solution of the equation by least squares estimation or other estimation methods in practice. Second, if \(\boldsymbol {W_{i}^{\mathrm {-1}}}\) does not exist, i.e., ∃k,w kk =0, we are not able to calculate v from f(v). In this case, we will exclude v k from the concept vectors because w kk =0 means that v k does not contribute to this similarity model since it is not helpful for further calculations.
6 Locating a concept in the concept space by its similarity position
From the above section, we know that there exists an isometry f between \(\mathfrak {C}\) and  . We call the mapped concept vectors in
. We call the mapped concept vectors in  as d-vectors. We use d
i
to denote the d-vector of a concept vector v
i
, i.e., d
i
=f(v
i
). So, a rewritten form of Corollary 1 is
as d-vectors. We use d
i
to denote the d-vector of a concept vector v
i
, i.e., d
i
=f(v
i
). So, a rewritten form of Corollary 1 is
In other words, the Euclidean distance between two d-vectors equals to the similarity-derived distance of the correspondent concept (vectors).
Reviewing Problem 1, now, we are going to find a function that can map a similarity position sp into a d-vector d given a set \(\mathfrak {D}\) of known d-vectors in  . Since sp can be converted to the distances from other points in the \(\mathfrak {D}\), the problem is similar to locating a point’s coordinates given its distance with other points in
. Since sp can be converted to the distances from other points in the \(\mathfrak {D}\), the problem is similar to locating a point’s coordinates given its distance with other points in  . Such problems have been discussed in distance geometry, which concerns some geometric concepts in terms of distances. The fundamental problem in distance geometry is the distance geometry problem (DGP) (Liberti et al. 2014).
. Such problems have been discussed in distance geometry, which concerns some geometric concepts in terms of distances. The fundamental problem in distance geometry is the distance geometry problem (DGP) (Liberti et al. 2014).
Given an integer K>0 and a simple undirected graph G=(V,E) whose edges are weighted by a nonnegative function \(\mathrm {d} : E\to \mathbb {R}_{+}\), determine whether there is a function \(\mathrm {x} : V \to \mathbb {R}^{K}\) such that ∀{u,v}∈E ∥x(u)−x(v)∥=d({u,v}).
Though started as a purely mathematical problem, DGP is gaining more and more popularity in bio-informatics, in which researchers use related algorithms to construct molecular structures. Our problem is also a sub-problem of DGP, which can be transformed into the following form:
Problem 2
How to find a function g ∗ s.t. \(\mathrm {g^{*}}(\mathfrak {D},\boldsymbol {p})=\boldsymbol {d_{j}}\), given
-
1.
The coordinates of all vectors in \(\mathfrak {D}\).
-
2.
The distance of a d-vector dp with all points in \(\mathfrak {D}\). The distances are denoted as a vector p in which p i =t∘s i (vp,v i ), where vp is the correspondent concept vector of dp.
The general DGP in N-dimension is NP-Hard. However, Dong and Wu (2002) suggest a method to solve the problem in O(|D|·N 3) if all the inter-point distance values are given. Using Dong’s method, we will first show a simple solution to our walk-through example in Section 3.3.
Since we have already known that the weight vector is (0.4472,0.8944), the d-vectors are d 1 =(0.4472,0.8944),d 2 =(0.4472,0), and d 3 =(0,0.8944). Given the similarity position (0,0.1056,0.5528), we can calculate the distance position as (1,0.8944,0.4472). So, we want to locate a point d 0 =(x,y) in the space which has a distance of 0.8944, 1, and 0.4472 with d 1 , d 2 , and d 3 respectively. Considering the definition of Euclidean distance, we will have
In order to solve x and y, let us minus Eq. 6 from Eqs. 7 and 8 to have the following two equations:
So, x=0 and y=0. Divide the coordinates with the weigh vector; we have the unknown concept x’s concept vector as (0,0).
Since Dong’s algorithm was designed for three dimension spaces, we will extend it to a general case of N-dimension in which N is the size of our distance vector as well as the number of attributes. The coordinates of any d-vectors d j (j∈[1,M]) in \(\mathfrak {D}\) are already known, in which M is the size of the concept space. To simplify our discussion, we will denote the unknown vector dp as d 0 . We can have the following representation of any d-vector d k in \(\mathfrak {D}\cup \{\boldsymbol {d_{0}}\}\).
The distance between any known d j and the unknown d 0 can be calculated as the following. Remember that p j is a component in p, which identifies the distance between d 0 and d j . So by definition, we have
Expanding the left-hand side of the equation, we will have Eq. 13.
Expand d 0 and d j in Eq. 13 in their full vector forms as in Eq. 11; we have the general distance constraint (Eq. 14).
Let us make a copy of Eq. 14 by setting j as 1.
Subtract Eq. 15 from 14, we will have
Through a closer look of Eq. 16, we can see that the right-hand side has nothing to do with d 0 , so the right-hand side value is known to us. On the left-hand side, u 01 to u 0N are the components of the unknown d 0 , while the “coefficients” of them can be calculated by d 1 and d j . So, let us create M copies of Eq. 16 with the values of j ranging from 1 to M. The equations form a linear equation system which can be rewritten as
A ∗=(a mn ) M×N and b ∗=(b 1,b 2,…,b M )T where
Theorem 7
\(\mathfrak {D}\) is a set of d-vectors, dp is a d-vector, and p is the distance position of dp. There exists a function \(\mathrm {g^{*}}\colon 2^{\mathfrak {D}}\times \mathfrak {P}\to \mathfrak {D}\) s.t. \(g^{*}(\mathfrak {D},\boldsymbol {p})=\boldsymbol {dp}\) if r a n k(A ∗)=r a n k(B ∗)=N, in which B ∗=[A ∗,b ∗ ].
Proof
Let g ′ be a function that will solve a linear equation system. For any p, we can construct correspondent A ∗ and b ∗ using p and \(\mathfrak {D}\). So, the domain and range of g ′ are the same as g ∗.
Since rank(A ∗)=rank(B ∗)=N, A ∗ d=b ∗ has only one solution d 0 . So, \(f'(\mathfrak {D},\boldsymbol {p})=\boldsymbol {d_{0}}\).
Also from Eq. 17, we can see that d 0 satisfies Eq. 13 for all vectors in \(\mathfrak {D}\). So, d 0 =dp, and consequently, g ′=g ∗. □
Having obtained the above theorem, we can reach the following theorem which answers Problem 1 directly.
Theorem 8
\((\mathfrak {C}_{1},\mathrm {t}\circ \mathrm {s_{i}})\) is a finite concept space. sp is a similarity position and vp is the correspondent concept vector. N is a finite number of attributes. There exists a function g s.t. \(g(\mathfrak {C}_{1},\mathrm {t\circ s},\boldsymbol {sp})=\boldsymbol {v}\) if the following conditions are true:
-
1.
\(\mathfrak {C_{1}}\) is scaling and translation invariant.
-
2.
r a n k(A ∗)=r a n k(B ∗)=N.
Proof
Since \(\mathfrak {C_{1}}\) is scaling and translation invariant, and N is a finite number, from Theorem 3, we know that there exists an isometry f from \(\mathfrak {C}\) to  .
.
Let \(\mathfrak {D}=\{\mathrm {f}(\boldsymbol {v})\}_{\forall \boldsymbol {v}\in \mathfrak {C_{1}}}\). We can then construct the distance position p=t(sp). From Lemma 7, we know g ∗ exists because r a n k(A ∗)=r a n k(B ∗)=N. So,
From Corollary 2, we know that f−1 exists. So,
Finally, \(\mathrm {g}(\mathfrak {C}_{1},\mathrm {t\circ s},\boldsymbol {sp})=\mathrm {f}^{-1}(g^{*}(\{\mathrm {f}(\boldsymbol {v})\}_{\forall \boldsymbol {v}\in \mathfrak {C_{1}}},\mathrm {t}(\boldsymbol {sp})))\). □
7 Transforming non-numerical attribute values
In real scenarios, some values are not numerical. In this case, we have to extend our framework to non-numerical values, mostly string values. We will first give some definitions for the sake of further discussion.
Definition 9
Let V i be the set of all possible values of an attribute a i . σ i :V i ×V i →[0,1] is a similarity function on V i .
A value mapping function is a bijective function  in which M≥1 s.t. ∀v
1,v
2∈V
i
, δ
i
(v
1,v
2)=∥m
i
(v
1)−m
i
(v
2)∥2
in which M≥1 s.t. ∀v
1,v
2∈V
i
, δ
i
(v
1,v
2)=∥m
i
(v
1)−m
i
(v
2)∥2
For a non-numerical concept vector v=(v 1,v 2,…,v N ), its numerical version is v ′=(m 1(v 1),m 2(v 2),…,m N (v N )), and the length of v ′ is \(\sum _{i=1}^{N}{|\mathrm {m_{i}}(v_{i})|}\). As in Section 5.2, we assume that the distance between two concepts is decomposable. It is also reasonable to assume that the distance of concepts depends on the distance of correspondent values. So, we have the following property for concepts c 1 and c 2.
Let v 1 be the concept vector of concept c 1, so v 1 =(m 1(v 1),m 2(v 2),…,m N (v N )). It is easy to see that \(\mathrm {d}(c_{1}, c_{2})=\tilde {\mathrm {d}}(\boldsymbol {v_{1}},\boldsymbol {v_{2}})\). Therefore, our mapping preserves the distance between the concepts.
In discussions of later sections, since we will concentrate on the construction of m i only, we drop the subscript i to simplify notations. Subsequently, we have the value set V, value mapping function m, and distance function δ.
7.1 M=1
A trivial case is that V is already numerical, as we have discussed in previous sections. So, m(v)=v if  .
.
Another case is that V is not numerical but it can be embedded into  , i.e., ∀v
1,v
2∈V,δ(v
1,v
2)=|m(v
1)−m(v
2)|. The following algorithm will construct m for each v in V.
, i.e., ∀v
1,v
2∈V,δ(v
1,v
2)=|m(v
1)−m(v
2)|. The following algorithm will construct m for each v in V.

Theorem 9
There exists a value mapping function m from V to  ⇔ Algorithm 1 can find m(v) for any v∈V.
⇔ Algorithm 1 can find m(v) for any v∈V.
Proof
Omitted. □
7.2 M>1
A more complicated situation is that V can only be mapped to \(\mathbb {R}^{M}\) in which M>1. We will first discuss a common but simple case here. For some attribute, its values are independent, i.e., for any two different values, their similarity/distance remain the same. So, we can map the value to a binary sequence, with each bit represents a value option.
If ∀v
1,v
2∈V δ(v
1,v
2)=d, we can construct the value mapping function  as the following:
as the following:
Obviously, m satisfies the definition of a value mapping function, because for any v 0≠v 1,
For other kinds of attributes, the problem to find a value mapping function is a general DGP problem. If we can find an embedding  , m satisfies the definition of a value mapping function. The problem is quite complicated, so we will only give the general condition here. Let S
∗ be the similarity matrix of value pairs in V
i
. According to Sippl and Scheraga (1986), S
∗ can be embedded in \(\mathbb {R^{K}}\) but not \(\mathbb {R}^{K-1}\) if and only if:
, m satisfies the definition of a value mapping function. The problem is quite complicated, so we will only give the general condition here. Let S
∗ be the similarity matrix of value pairs in V
i
. According to Sippl and Scheraga (1986), S
∗ can be embedded in \(\mathbb {R^{K}}\) but not \(\mathbb {R}^{K-1}\) if and only if:
-
There is a principal (K+1)×(K+1) submatrix D∈S ∗, the Cayley-Menger determinant of D is non-zero.
-
For μ∈2,3, every principal (K+μ)×(K+μ) submatrix E that includes D has zero Cayley-Menger determinant.
8 Further discussions: preliminary implementation examples
The direct application of our framework is to solve our prime problem, which is a kind of attribute mining task. We will first show a mini example which involves an initial implementation of our methods as well as several interesting test cases in this section. In the second part of the section, we will discuss the outline and difficulties of an ongoing attribute mining experiment.
8.1 A mini example
We will take a mini example to show an initial implementation to our geometric method. Given a small set of concepts (called instances) which have only binary attributes, we tried to find the attributes of a new concept based on its similarity with the instances. This set of instances is from the formal concept analysis (FCA) domain (Wille 1984). The set shown in Fig. 1 contains eight concepts of water-related plants and animals. Each concept has nine attributes. To simplify further discussions, we refer to the first attribute “needs water to live” as a 1, “lives in water” as a 2, and so on.
“Live in water” example (http://www.upriss.org.uk/fca/examples.html)
8.1.1 The initial implementation
We have completed the initial implementation of the following steps:
8.1.1.1 Creating the similarity function
We used the UMBC Phrase Similarity Service (Han et al. 2013b) to calculate similarity. The service has two types: concept similarity and relation similarity. Our similarity function s is a hybrid of the two types.
In the above equation, s 1 and s 2 are the concept and relation similarity functions respectively. α is set to 0.5 initially. The distance function d is set as d(a,b)=1−s(a,b).
8.1.1.2 Finding an approximation to the isometry function
Following discussions in Section 5.3, we used a linear weighting function f to approximate the isometry from the concept space of instances to a Euclidean space. Let us recall Eq. 5:
Given a set of v and the distances between them, to solve w kk could be viewed as a linear regression problem, which was solved by Ridge regression. We refer to w kk as w k in following discussions.
8.1.1.3 Finding the attributes of a concept
-
1.
We found the similarity of the given concept to the instances and transformed the similarity values into distance values.
-
2.
The concept vectors of instances were transformed to d-vectors by the linear weighting function.
-
3.
Following Eq. 17 in Section 6, we set up a system of linear equations and get the slack solution by least squares.
-
4.
Since the attributes are binary, we discretized the result vector. The discretization function employed the following equation.
$$ v_{i} = \left\{\begin{array}{ll} 1&v_{i}\geq \beta\\ 0&v_{i}<\beta\\ -1&w_{i}^{2}=0\\ \end{array} \right. $$(23)v i =−1 means the instances cannot predict the value of v i , because w i =0, which means that the ith attribute does not contribute to the similarity.
8.1.2 Test cases
Because there is no “bream” in the UMBC vocabulary, we substituted it with “trout” with the same attributes (Table 1). Setting α=0.5, let us first take a look at the weights of the linear weighting function trained. We will see that there are three abnormal values. \(w_{1}^{2}\) is 0 because for all concepts, a 1 is always 1, so it does not contribute to the calculation of similarity. \(w_{5}^{2}\) and \(w_{6}^{2}\) have negative values which can only be resulted from approximation errors. Maybe since a 5 and a 6 concern about two biology terms “monocotyledon” and “dicotyledon,” they have little impact on some similarity measurement. In practice, we set negative weights such as \(w_{5}^{2}\) and \(w_{6}^{2}\) to 0.
We first tried four concepts which are not very similar to existing instances. They were “swan,” “buffalo,” “water lily,” and “dolphin.” Table 2 shows the results for the five concepts. We can see that in these test cases, the majority of attributes are correct, but still, there are some errors.
We also extended the test cases a bit. We created a concept set of 50 concepts including the original eight concepts. The concepts are all animals or plants related to water. We performed ten times fivefold cross validations on the data set. The correctness is measured on the attribute level using the following equation. Since a 1, a 5, and a 6 contribute little to similarity measurement as we have discussed before, we did not evaluate these 3 attributes.
The results of the experiment are shown in Table 3. The best result (0.760) comes from Setting 2 where α=0.5 and β=0.2. For all the ten cross validations, the results remain quite consistent. For all settings, β is 0.2 because we found that changing β from 0.2 to 1 does not impact our result much. Settings 1 to 3 differed in the value of α. From the results, we can see that the hybrid model outperforms concept model or relation model. Setting 4 used ordinary least squares instead of Ridge regression. The result shows that there is not much difference between these two. Setting 5 used the logarithm-based function to transform similarity value to distance value, s.t. t(x)=− log(x) instead of t(x)=1−x. We can see that this lowered the performance significantly. We guess t(x)=− log(x) is not an ideal transformation function for this similarity model.
We want to emphasize that by this preliminary experiment, we do not intend to show how good the performance of current implementation is, because of the scale and nature of data. On the contrary, our implementation needs much improvement, which is shown in the next section. However, this experiment does shed some light on the potential of our geometry-based method in applications.
8.2 Extension to an attribute mining experiment: outline and difficulties
In order to expand the abovementioned mini example for further experiment, one instant thought is to find a data set from real-world applications. We are mining the attributes for consumer products, whose attributes could be retrieved from a B2C website, such as JD.com. We focus on the products because of two reasons. First, product names contain little polysemy. Second, product attributes on B2C websites are usually quite detailed.
For data preparation, we select products from several related categories like computers and digital devices. Since the attributes generally take string values, we transform the attribute by methods derived from Section 7.2. We also tried to prune the data for consistency.
The similarity model (Liu and Duan 2015) consists of two components: a relational model and a hierarchy model. The relational model is based on the PMI-IR of two products, while the hierarchy model based on the category on the JD.com. The other algorithms are the same with those in the mini example.
Because this is an ongoing task, we will list some difficulties and future prospects.
-
The product attributes listed on the website are not always attributes in a strict sense. Some of the attributes are “basket” attributes, such as “characteristics,” which is too vague to be considered in the experiment. Moreover, different attribute names may refer to the same attribute.
-
We need a “fine-grained” similarity model to capture the difference between within one category because product attributes listed on the website only represent part of the intension of the product. Generally, it is the part that it differs with other products in the same category. An initial idea is to combine different similarity models, especially those utilizes different resources, such as ontology or corpus (word vectors).
-
We need better methods to estimate the isometry, since a simple regression may not be that accurate. Therefore, it may be useful to exploit new “kernel functions” for the mapping, similar to those in support vector machines.
9 Conclusions
In this paper, we have introduced the computing of concepts in a vector space. We have shown how to construct a function to map a concept’s similarity position to its concept vector by embedding the concept space into a Euclidean space. Then, we have proved that under some given conditions, both the function and the embedding do exist. We have also discussed how to handle non-numerical attributes. We have shown some preliminary experimental results and shared some difficulties in implementation. Our results will benefit future works in attribute retrieval.
This work is on its early stage. We are still facing some difficulties. Theoretically, one problem is that the proposed conditions on matrix ranks are quite strong. For future studies, we would like to find if there are alternative weaker conditions. In practice, it is not actually so easy to find the isometry. Though we have suggested using linear regression for approximation, we may take advantage of other machine learning methods. In a worse scenario, the weight matrix may even not exist. In this case, we will try to find another mapping function from concept vectors to d-vectors other than the linear weight function.
10 Endnote
1 Jin et al. (2014) note that if the similarity model satisfies triangle inequality, the distance function 1−s also does. Our proof actually contradicts their result.
References
Adams, Benjamin, and Martin Raubal. 2009. A metric conceptual space algebra. In International Conference on Spatial Information Theory, ed. Kathleen S. Hornsby, Christophe Claramunt, Michel Denis, and Gérard Ligozat, 51–68. Berlin, Heidelberg: Springer.
Agirre, Eneko, Enrique Alfonseca, Keith Hall, Jana Kravalova, Marius Paşca, and Aitor Soroa. 2009. A study on similarity and relatedness using distributional and WordNet-based approaches. In Proceedings of Human Language Technologies: The 2009 Annual Conference of the North American Chapter of the Association for Computational Linguistics, 19–27. Stroudsburg: Association for Computational Linguistics.
Alfonseca, Enrique, Marius Pasca, and Enrique Robledo-Arnuncio. 2010. Acquisition of instance attributes via labeled and related instances. In Proceeding of the 33rd international ACM SIGIR conference on Research and development in information retrieval, 58–65. New York: ACM.
Artiles, Javier, Andrew Borthwick, Julio Gonzalo, Satoshi Sekine, and Enrique Amigó. 2010. WePS-3 evaluation campaign: overview of the web people search clustering and attribute extraction tasks. Paper presented at Proceedings of the Third Web People Search Evaluation Forum (WePS-3). Padua: CLEF 2010.
Artiles, Javier, Julio Gonzalo, and Satoshi Sekine. 2009. Weps 2 evaluation campaign: overview of the web people search attribute extraction task. Paper presented at 2nd Web People Search Evaluation Workshop (WePS 2009), 18th WWW Conference. Madrid.
Baroni, Marco, Georgiana Dinu, and Germán Kruszewski. 2014. Don’t count, predict! A systematic comparison of context-counting vs. context-predicting semantic vectors. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, 238–247. Stroudsburg: Association for Computational Linguistics.
Baroni, Marco, and Alessandro Lenci. 2010. Distributional memory: A general framework for corpus-based semantics. Computational Linguistics 36(4):673–721.
Baroni, Marco, and Alessandro Lenci. 2011. How we blessed distributional semantic evaluation. In Proceedings of the GEMS 2011 Workshop on GEometrical Models of Natural Language Semantics, 1–10. Stroudsburg: Association for Computational Linguistics.
Baroni, Marco, Brian Murphy, Eduard Barbu, and Massimo Poesio. 2010. Strudel: A corpus-based semantic model based on properties and types. Cognitive Science 34(2):222–254.
Bellare, Kedar, Partha Pratim Talukdar, Giridhar Kumaran, Fernando Pereira, Mark Liberman, Andrew McCallum, and Mark Dredze. 2007. Lightly-supervised attribute extraction. In NIPS 2007 Workshop on Machine Learning for Web Search, 1–7.
Blackburn, Patrick. 1993. Modal logic and attribute value structures. In Diamonds and Defaults, Synthese Library, ed. Maarten de Rijke, 19–65. Berlin, Heidelberg: Kluwer Academic Publishers Group.
Bollegala, Danushka, Yutaka Matsuo, and Mitsuru Ishizuka. 2007. Measuring semantic similarity between words using web search engines. In WWW ’07: Proceedings of the 16th International Conference on World Wide Web, 757–766. New York: ACM.
Brin, Sergey. 1999. Extracting patterns and relations from the world wide web. In The World Wide Web and Databases, ed. Paolo Atzeni, Alberto Mendelzon, and Giansalvatore Mecca, 172–183. London: Springer-Verlag.
Budanitsky, Alexander, and Graeme Hirst. 2001. Semantic distance in WordNet: An experimental, application-oriented evaluation of five measures. In Workshop on WordNet and Other Lexical Resources, Second Meeting of the North American Chapter of the Association for Computational Linguistics, 29–34. Stroudsburg: Association for Computational Linguistics.
Bullinaria, John A., and Joseph P. Levy. 2007. Extracting semantic representations from word co-occurrence statistics: A computational study. Behavior Research Methods 39(3):510–526.
Chen, Hsin-Hsi, Ming-Shun Lin, and Yu-Chuan Wei. 2006. Novel association measures using web search with double checking. In Proceedings of the 21st International Conference on Computational Linguistics and the 44th annual meeting of the ACL, Association for Computational Linguistics Morristown, 1009–1016. Stroudsburg: Association for Computational Linguistics.
Dong, Qunfeng, and Zhijun Wu. 2002. A linear-time algorithm for solving the molecular distance geometry problem with exact inter-atomic distances. Journal of Global Optimization 22(1-4):365–375.
Erk, Katrin. 2012. Vector space models of word meaning and phrase meaning: a survey. Language and Linguistics Compass 6(10):635–653.
Fellbaum, Christiane. 1998. WordNet. Cambridge: MIT Press.
Finkelstein, Lev, Evgeniy Gabrilovich, Yossi Matias, Ehud Rivlin, Zach Solan, Gadi Wolfman, and Eytan Ruppin. 2001. Placing search in context: the concept revisited. In Proceedings of the 10th International Conference on World Wide Web, 406–414. New York: ACM.
Frixione, Marcello, and Antonio Lieto. 2013. Dealing with concepts: from cognitive psychology to knowledge representation. Frontiers of Psychological and Behevioural Science 2(3):96–106.
Gao, Jian-Bo, Bao-Wen Zhang, and Xiao-Hua Chen. 2015. A WordNet-based semantic similarity measurement combining edge-counting and information content theory. Engineering Applications of Artificial Intelligence 39:80–88.
Gärdenfors, Peter. 2004. Conceptual spaces: The geometry of thought. Cambridge: MIT press.
Gärdenfors, Peter. 2014. The geometry of meaning: Semantics based on conceptual spaces. Cambridge: MIT Press.
Gärdenfors, Peter, and Mary-Anne Williams. 2001. Reasoning about categories in conceptual spaces. In Proceedings of the Fourteenth International Joint Conference of Artificial Intelligence, 385–392. San Francisco: Morgan Kaufmann Publishers Inc.
Gentner, Dedre. 1983. Structure-mapping: A theoretical framework for analogy. Cognitive Science 7(2):155–170.
Ghani, Rayid, Katharina Probst, Yan Liu, Mark Kremao, and Andrew Fano. 2006. Text mining for product attribute extraction. ACM SIGKDD Explorations Newsletter 8(1):41–48.
Hahn, Ulrike, and Nick Chater. 1997. Concepts and similarity. In Knowledge, concepts and categories, ed. Koen Lamberts and David Shanks, 43–92. East Sussex: Psychology Press.
Han, Lushan, Tim Finin, Paul McNamee, Akanksha Joshi, and Yelena Yesha. 2013a. Improving word similarity by augmenting PMI with estimates of word polysemy. IEEE Transactions on Knowledge and Data Engineering 25(6):1307–1322.
Han, Lushan, Abhay L. Kashyap, Tim Finin, James Mayfield, and Johnathan Weese. 2013b. UMBC ebiquity-core: Semantic textual similarity systems. In Proceedings 2nd Joint Conference on Lexical and Computational Semantics, 44–52. Stroudsburg: Association for Computational Linguistics.
Harris, Zellig S. 1954. Distributional structure. Word 10(2-3):146–162.
Janowicz, Krzysztof, Martin Raubal, and Werner Kuhn. 2012. The semantics of similarity in geographic information retrieval. Journal of Spatial Information Science 2011(2):29–57.
Jiang, Jay J., and David W. Conrath. 1997. Semantic similarity based on corpus statistics and lexical taxonomy. In Proceedings of International Conference on Research in Computational Linguistics, 19–33. Stroudsburg: Association for Computational Linguistics.
Jin, Peng, Likun Qiu, Xuefeng Zhu, and Pengyuan Liu. 2014. A hypothesis on word similarity and its application. In Chinese Lexical Semantics, ed. Xinchun Su and Tingting He, 317–325. Cham: Springer.
Kopliku, Arlind, Mohand Boughanem, and Karen Pinel-Sauvagnat. 2011. Towards a framework for attribute retrieval. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, ed. Bettina Berendt, Arjen de Vries, Wenfei Fan, Craig Macdonald, Iadh Ounis, and Ian Ruthven, 515–524. New York: ACM.
Li, Yuhua, Zuhair A. Bandar, and David McLean. 2003. An approach for measuring semantic similarity between words using multiple information sources. IEEE Transactions on Knowledge and Data Engineering 15(4):871–882.
Liberti, Leo, Carlile Lavor, Nelson Maculan, and Antonio Mucherino. 2014. Euclidean distance geometry and applications. SIAM Review 56(1):3–69.
Lieto, Antonio, Andrea Minieri, Alberto Piana, and Daniele P. Radicioni. 2015. A knowledge-based system for prototypical reasoning. Connection Science 27(2):137–152.
Liu, Bing. 2011. Opinion mining and sentiment analysis. In Web Data Mining, ed. Bing Liu, 459–526. Berlin Heidelberg: Springer.
Liu, Hui, and Jianyong Duan. 2015. Attribute construction for online products by similarity computing. ICIC Express Letters 9(1):99–105.
Liu, Hongzhe, Hong Bao, and De Xu. 2012. Concept vector for semantic similarity and relatedness based on WordNet structure. Journal of Systems and Software 85(2):370–381.
McRae, Ken, George S. Cree, Mark S. Seidenberg, and Chris McNorgan. 2005. Semantic feature production norms for a large set of living and nonliving things. Behavior Research Methods 37(4):547–559.
Medin, Douglas L., Robert L. Goldstone, and Dedre Gentner. 1990. Similarity involving attributes and relations: judgments of similarity and difference are not inverses. Psychological Science 1(1):64–69.
Mihalcea, Rada, Courtney Corley, and Carlo Strapparava. 2006. Corpus-based and knowledge-based measures of text semantic similarity. In Proceedings of the 21st Conference on Artificial Intelligence, vol. 1, ed. Anthony Cohn, 775–780. Cambridge: AAAI Press.
Miller, George A., and Walter G. Charles. 1991. Contextual correlates of semantic similarity. Language and Cognitive Processes 6(1):1–28.
Mitchell, Jeff, and Mirella Lapata. 2008. Vector-based models of semantic composition. In Proceedings of the 46th Annual Meeting of the Association for Computational Linguistics, 236–244. Stroudsburg: Association for Computational Linguistics.
Nagy, István, Richárd Farkas, and Márk Jelasity. 2009. Researcher affiliation extraction from homepages. In Proceedings of the 2009 Workshop on Text and Citation Analysis for Scholarly Digital Libraries, 1–9. Stroudsburg: Association for Computational Linguistics.
Nosofsky, Robert M. 1986. Attention, similarity, and the identification–categorization relationship. Journal of Experimental Psychology: General 115(1):39–57.
Nosofsky, Robert M. 1992. Similarity scaling and cognitive process models. Annual Review of Psychology 43(1):25–53.
Pang, Bo, and Lillian Lee. 2008. Opinion mining and sentiment analysis. Foundations and Trends®; in Information Retrieval 2(1–2):1–135.
Pasca, Marius, and Benjamin V. Durme. 2007. What you seek is what you get: Extraction of class attributes from query logs. In Proceedings of the 20th International Joint Conference on Artificial Intelligence (IJCAI-07), ed. Rajeev Sangal, Harish Mehta, and R. K. Bagga, 2832–2837. San Francisco: Morgan Kaufmann Publishers Inc.
Petrakis, Euripides G.M., Giannis Varelas, Angelos Hliaoutakis, and Paraskevi Raftopoulou. 2006. X-similarity: Computing semantic similarity between concepts from different ontologies. Journal of Digital Information Management 4(4):233–237.
Probst, Katharina, Rayid Ghani, Marko Krema, Andrew Fano, and Yan Liu. 2007. Semi-supervised learning of attribute-value pairs from product descriptions. In Proceedings of the 20th International Joint Conference on Artificial Intelligence (IJCAI-07), ed. Rajeev Sangal, Harish Mehta, and R. K. Bagga, 2838–2843. San Francisco: Morgan Kaufmann Publishers Inc.
Raubal, Martin. 2004. Formalizing conceptual spaces. In Formal Ontology in Information Systems, Proceedings of the Third International Conference (FOIS 2004), ed. Achille C. Varzi and Laure Vieu, 153–164. Amsterdam: IOS Press.
Reisberg, Daniel. 2013. The Oxford handbook of cognitive psychology. Oxford: University Press.
Resnik, Philip. 1995. Using information content to evaluate semantic similarity in a taxonomy. In Proceedings of the 14th International Joint Conferences on Artificial Intelligence, ed. Chris S. Mellish, 448–453. San Francisco: Morgan Kaufmann Publishers Inc.
Rodríguez, M. Andrea, and Max J. Egenhofer. 2003. Determining semantic similarity among entity classes from different ontologies. IEEE Transactions on Knowledge and Data Engineering 15(2):442–456.
Sahlgren, Magnus. 2005. An introduction to random indexing. Paper presented at Methods and Applications of Semantic Indexing Workshop at the 7th International Conference on Terminology and Knowledge Engineering. Copenhagen: TKE.
Sánchez, David, Montserrat Batet, David Isern, and Aida Valls. 2012. Ontology-based semantic similarity: A new feature-based approach. Expert Systems with Applications 39(9):7718–7728.
Santus, Enrico, Emmanuel Chersoni, Alessandro Lenci, Chu-Ren Huang, and Philippe Blache. 2016. Testing APSyn against vector cosine on similarity estimation. In Proceedings of the 30th Pacific Asia Conference on Language, Information and Computation, Korean Society for Language and Information, 229–238. Seoul.
Santus, Enrico, Qin Lu, Alessandro Lenci, and Chu-Ren Huang. 2014. Unsupervised antonym-synonym discrimination in vector space. In First Italian Conference on Computational Linguistics (CLiC-it 2014), ed. Roberto Basili, Alessandro Lenci, and Bernardo Magnini, 328–333. Pisa: Pisa University Press.
Sekine, Satoshi. 2008. Extended named entity ontology with attribute information. In Proceedings of the Sixth International Language Resources and Evaluation (LREC ’08), ed. Nicoletta Calzolari, Khalid Choukri, Bente Maegaard, Joseph Mariani, Jan Odijk, Stelios Piperidis, and Daniel Tapias, 52–57. Paris: European Language Resources Association.
Shepard, Roger N. 1987. Toward a universal law of generalization for psychological science. Science 237(4820):1317–1323.
Sippl, Manfred J., and Harold A. Scheraga. 1986. Cayley-Menger coordinates. Proceedings of the National Academy of Sciences of the United States of America 83(8):2283–2287.
Suchanek, Fabian M., Gjergji Kasneci, and Gerhard Weikum. 2008. Yago: A large ontology from wikipedia and WordNet. In Web Semantics: Science, Services and Agents on the World Wide Web, 203–217.
Tokunaga, Kosuke, Jun’ichi Kazama, and Kentaro Torisawa. 2005. Automatic discovery of attribute words from web documents. In Proceedings of the Second International Joint Conference on Natural Language Processing (IJCNLP-05), ed. Robert Dale, Kam-Fai Wong, Jian Su, and Oi Yee Kwong, 106–118. Berlin, Heidelberg: Springer-Verlag.
Turney, Peter D. 2006. Similarity of semantic relations. Computational Linguistics 32(3):379–416.
Turney, Peter D., and Patrick Pantel. 2010. From frequency to meaning: Vector space models of semantics. Journal of Artificial Intelligence Research 37(1):141–188.
Tversky, Amos. 1977. Features of similarity. Psychological Review 84(4):327–352.
Varelas, Giannis, Epimenidis Voutsakis, Paraskevi Raftopoulou, Euripides G.M. Petrakis, and Evangelos E. Milios. 2005. Semantic similarity methods in WordNet and their application to information retrieval on the web. In Proceedings of the 7th annual ACM international workshop on Web information and data management, 10–16. New York: ACM.
Vigliocco, Gabriella, David P. Vinson, William Lewis, and Merrill F. Garrett. 2004. Representing the meanings of object and action words: the featural and unitary semantic space hypothesis. Cognitive Psychology 48(4):422–488.
Wille, Rudolf. 1984. Liniendiagramme hierarchischer begriffssysteme. Anwendungen der Klassifikation: Datenanalyse und numerische Klassifikation, 32–51. Frankfurt: Indeks-Verlag.
Wu, Zhibiao, and Martha Palmer. 1994. Verbs semantics and lexical selection. In Proceedings of the 32nd Annual Meeting on Association for Computational Linguistics, 133–138. Stroudsburg: Association for Computational Linguistics.
Acknowledgements
This work is supported by the Ministry of Education of China (Project of Humanities and Social Sciences, Grant No. 13YJC740055) and the National Science Foundation of China (Grant No. 61672040).
This paper is an extended version of “Hui Liu and Jianyong Duan (2016), An Analysis of the Relation between Similarity Positions and Attributes of Concepts by Distance Geometry, in the Proceedings of the 17th Chinese Lexical Semantics Workshop (CLSW2016), Singapore, pp. 432–441”.
Author information
Authors and Affiliations
Contributions
Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, H., Duan, J. Geometric analysis of concept vectors based on similarity values. lingua. sin. 3, 12 (2017). https://doi.org/10.1186/s40655-017-0029-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40655-017-0029-0
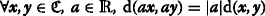
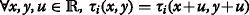 .
.